2.2 The Electron configuration

2.2 The Electron configuration

Quantum mechanical model of Atom: 

It is based on Heisenberg’s uncertainty principle and Schrodinger’s equation. This model helps to understand the electronic structure of an atom more precisely. It explains the address of an electron inside an atom in the form of quantum numbers.

Principle Quantum Number:

It is denoted by “n”. It tells us about the energy and the distance of an electron from the nucleus.

So far we have 7 periods in periodic table hence 7 energy levels can be understood. Each energy level is related to each period.

These shells can also be designated as K L M N O P Q etc.

Azimuthal Quantum Number: 

It is denoted by “l”. It’s value depends on Principle Quantum Number n.  It tells us about sublevel of a shell that is subshell.

For each value of n, l= 0 to n-1.

So

n=1 means l=0  means “s” subshell

n=2means l=0, 1 means “s” and “p” subshells

n=3 means l=0, 1,2 means “s”, “p”  and “d”  subshells

n=4 means l=0, 1,2,3 means “s”, “p” , “d” and  “f”   subshells

n=5 means l=0, 1,2,3,4 means “s”, “p” , “d”, “f”  and “g” subshells  and so on…….

Magnetic Quantum Number: 

It is denoted by “m”. It tells us about the orbitals. Each value of l corresponds to one orbital.

 For each value of “l” m= -l to +l on number line.

So l=0 means m=0 means only one value means one orbital.

S subshell has only one orbital.

Spin Quantum Number:

It is denoted by “s” and has two values for each value of m,

+1/2(Clockwise spin) and -1/2(anticlockwise spin) which means two elctrons.

Principle(n)	Azimuthal(l=0 to n-1)	Subshell	Magnetic(m=-l,0,+l)	e
1	0	s	0	2
2	0,1	s,p	0,-1,0,+1	8
3	0,1,2	s,p,d	0,-1,0,1,-2,-1,0,1,2	18
4	0,1,2,3	s,p,d,f	0,-1,0,1,-2,-1,0,1,2,-3,-2,-1,0,1,2,3	32

Thus we seen that p subshell start with n=2, d subshell starts with n=3 and f subshell starts with n=4.

Heisenberg uncertainty principle, it is impossible to determine momentum and position of an electron in an atom simultaneously.

 If position is to determine its momentum will change and vice versa because light(energy) is to be dropped on an electron to track it, which will change the position of the electron.

Momentum (p) = mass(m) x Velocity(v)

Hence if its not possible to determine the position of an electron , how can we say that electron revolve around the nucleus in discrete orbits. We can only find the probability of electron in some space, called orbital.

What is Schrodinger wave equation? :

Erwin Schrodinger gave a mathematical equation “Schrodinger wave equation”for the wave nature of electron   Ĥψ = E ψ where H is Hamiltonian operator and E is total energy operator.

Solution of this equation using super computer gives numerical solutions,  which we call as quantum numbers.

Hund’s Rule of Maximum Multiplicity

Hund’s Rule of Maximum Multiplicity suggests that Pairing of electrons does not take place until all the orbitals of a sub-shell are singly filled.

Pauli’s Exclusion principle for electronic configuration

Pauli’s Exclusion principle for electronic configuration suggests that No Two electrons can have same set of four quantum numbers. It means that an orbital can only have two electrons. This principle is used to write the orbital diagram of atoms along with Hund’s Rule of maximum multiplicity and Aufbau rule.

Aufbau Principle and filling of electrons in orbitals and sub shells

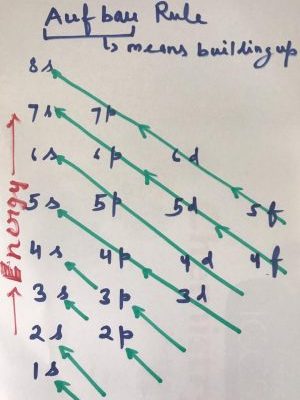
Aufbau Principle for electronic configuration is not on the name of any scientist as usually happened in sciences. Aufbau means building up.

Electrons are build up in orbitals of different subshells of different energy levels on the basis of energy.

Electrons first fill lower energy level and then move to next higher level.

                                                          s orbitals

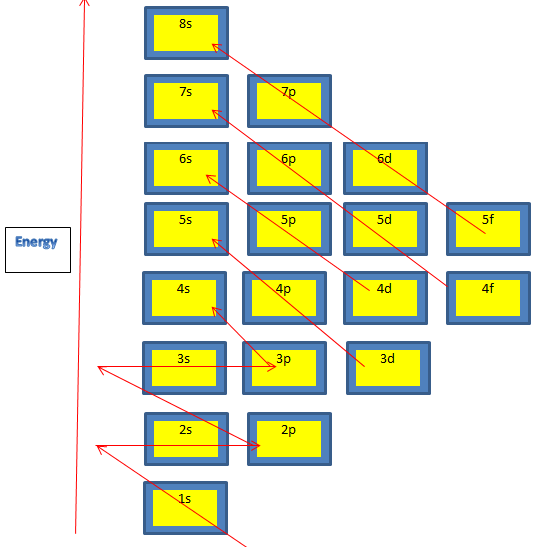
So electrons start filling from 1s orbital on wards in the following sequence:

1s,2s,2p , 3s,3p,4s,3d,4p,5s,4d,5p,6s,4f,5d,6p,7s,5f,6d,7p,8s

Simply it can be learned as ssp sps dps dps fdps fdps

Atomic Number	Element	Electronic Configuration
1	Hydrogen	Is1
2	Helium	Is2
3	Lithium	1s2 2s1
4	Beryllium	1s2 2s2
5	Boron	1s2 2s2 2p1
6	Carbon	1s2 2s2 2p2
7	Nitrogen	1s2 2s2 2p3
8	Oxygen	1s2 2s2 2p4
9	Fluorine	1s2 2s2 2p5
10	Neon	1s2 2s2 2p6
11	Sodium	1s22s22p63s1
12	Magnesium	1s22s22p63s2
13	Aluminium	1s22s22p63s23p1
14	Silicon	1s22s22p63s23p2
15	Phosphorus	1s22s22p63s23p3
16	Sulphur	1s22s22p63s23p4
17	Chlorine	1s22s22p63s23p5
18	Argon	1s22s22p63s23p6
19	Potassium	1s22s22p63s23p64s1
20	Calcium	1s22s22p63s23p64s2
21	Scandium	1s22s22p63s23p64s2 3d1
22	Titanium	1s22s22p63s23p64s2 3d2
23	Vanadium	1s22s22p63s23p64s2 3d3
24	Chromium	1s22s22p63s23p64s1 3d5
25	Manganese	1s22s22p63s23p64s2 3d5
26	Iron	1s22s22p63s23p64s2 3d6
27	Cobalt	1s22s22p63s23p64s2 3d7
28	Nickel	1s22s22p63s23p64s2 3d8
29	Copper	1s22s22p63s23p64s1 3d10

Shapes of Atomic orbitals of shells:

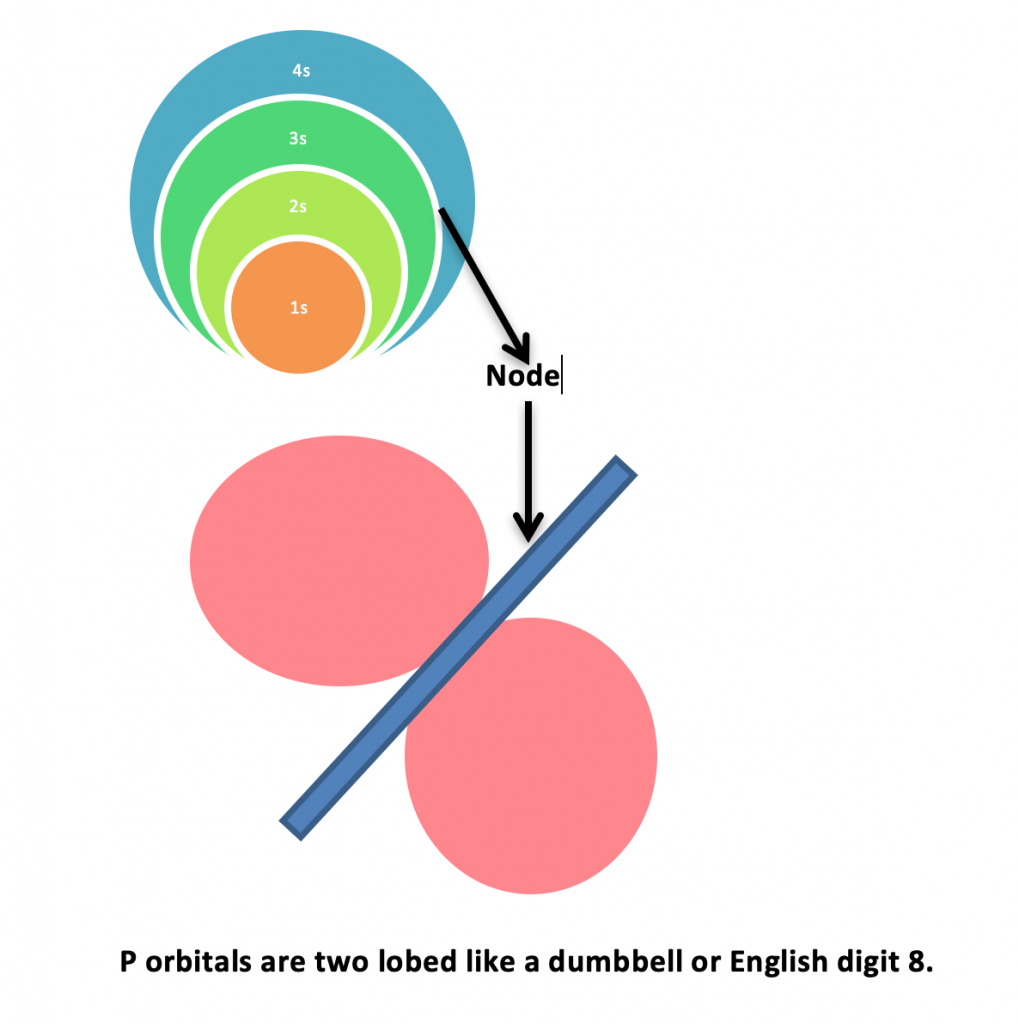
MainlyShapes of Atomic orbitals of shells include “s” Orbitals and “p” orbitals .

s orbitals are spherical in shapes. They are concentric which means one orbital in to other. Node is the space between two s orbitals where electrons probability is zero. Just for understanding, the white circular space between spheres is node.

p orbitals have two lobes dumbbell shape or English number 8 shape. The electrons probability is only with in the space of lobes because Nodes do not have any electron probability.

Orbital diagram

Nitrogen

1s2 2s2 2p3

So by now you have learned 2.2 The electron configuration of atoms.

You can read chemistry IA ideas here.